 architecture
architecture
前言
本期将导读Partial Information Decomposition这一篇论文,介绍信息分解方法。
信息分解这一概念由Randall Beer提出,毕业于CWRU,CS PhD,主要研究方向包括认知科学、信息论等。

动机
对于机器学习问题,假如均为布尔变量,有下述等式分别为: $$Z=X=Y$$ $$Z=X+Y$$ $$Z=X \oplus Y$$
对应的参数/架构分别需要1个(1层),2个(1层),2个(2层,异或问题不能通过单层感知机来解决)
直观理解为得到的信息有效性不同,比如已知$X=1$,则代入三个等式中分别得出$Z=1$,$Z>=1$,以及无任何关于$Z$的信息(需要同时得到$Y$,观测两变量间高阶相互作用)。
是否可以得到一个衡量信息大小的指标?需要创造一个方法来描述源变量和目标变量之间信息流动的结构。
以此为例,可以得到$Z$作为目标变量,$X$和$Y$作为源变量。
对于三个等式,信息结构可以通过下述方式描述:
- $X$提供了1比特的信息,$Y$也提供了同样的信息($Y$提供的信息是冗余的,redundant)
- $X$提供了1比特的信息,$Y$提供了其他1比特的信息($X$和$Y$提供的信息是单独的,unique,各不相同)
- $X$和$Y$一起提供了1比特的信息($X$和$Y$提供的信息是协同的,synergistic)
条件互信息
互信息的定义可以查看因果涌现 Part1 有效信息这篇文章,可以简单理解为熵减少的量,在此不重复赘述。
条件互信息:用于描述第三个变量已经给定的情况下,重新观测原有两变量的互信息
$$I(X;Y|Z)=\sum_z P(z)\sum_x \sum_y P(x,y) \log \frac{P(x,y|z)}{P(x|z)P(y|z)}$$
例:$X=Y=Z$, $I(X;Y)=1$, $I(X;Y|Z)=0$
如果有冗余信息,$I(X;Y|Z)<I(X;Y)$
例:$X=Y \oplus Z$, $I(X;Y)=0$, $I(X;Y|Z)=1$
如果有协同信息,$I(X;Y|Z)>I(X;Y)$
但结论逆推不成立,因为协同和冗余可能同时存在,所以需要一种方法来量化协同信息与冗余信息
冗余信息计算
基本概念
假设有$R={R_1,R_2,…,R_N}$作为源变量,目标变量$S$
$A_1, A_2, …, A_k$作为非空且可能相交的$R$的子集,共$2^N-1$个
拿出每一个子集,分别计算互信息 $$I(S;A_i)=\sum_s p(s) I(S=s;A_i)$$
源变量集合中计算得出的最小冗余信息(最少能提供的冗余信息)即为定义
$$I_{min}(S;A_1,A_2, …, A_k)=\sum_s p(s) \min_{A_i}I(S=s, A_i)$$
注:加权的不是具体的$a_i$,而是谁给outcome提供的信息量最小就加权谁,并非在最外面直接套一层$\min$
案例研究
例:$R_1=R_2=S$, $I_{min}(S;A_1,A_2)=1bit$
例:$S=R_1 \oplus R_2$, $I_{min}(S;A_1,A_2)=0bit$
问:冗余信息是从哪来的?是否来源于某个隐藏的公共变量(hidden common variable,可参考因果发现部分术语)或者混杂因子(confounder)?
例:a -> b a -> c b -> d c -> d b和c有共同混杂因子a
答:实际上存在b和c相互独立的情况,下面将以与门为例进行说明
例:$S=R_1 \& R_2$, $I_{min}(S;A_1,A_2)=\frac{3}{2}-\frac{3}{4}log_23bit$
冗余信息的属性:
- 非负性
- $$I_{min}(Z;{A_1,A_2, …, A_k}) \leq I(Z;A_i)$$
- $$I_{min}(Z;{A_1}) = I(Z;A_1)$$
冗余晶格
文氏图形式
此处重新定义能够计算冗余信息的$A_k$,每个之中可以有多个变量 $$A_1={{R_1},{R_2}}, A_2={R_1}, A_3={R_2}, A_4= {{R_1,R_2}}$$
对应关系:
$A_1$, $A_2$, $A_3$, $A_4$分别对应图中的{1}{2}, {1}, {2}. {12}
辨析:
- $A_1$是一个两个元素的集合,冗余信息即两个元素$R_1$,$R_2$之间的冗余信息
- $A_4$集合中只有一个元素,冗余信息即其和$S$之间的互信息,参考冗余信息属性3
- {12}可以理解为把二者看成一个二维变量,类似
concat,$R_1$和$R_2$要能观测到就都能观测到,要观测不到就都观测不到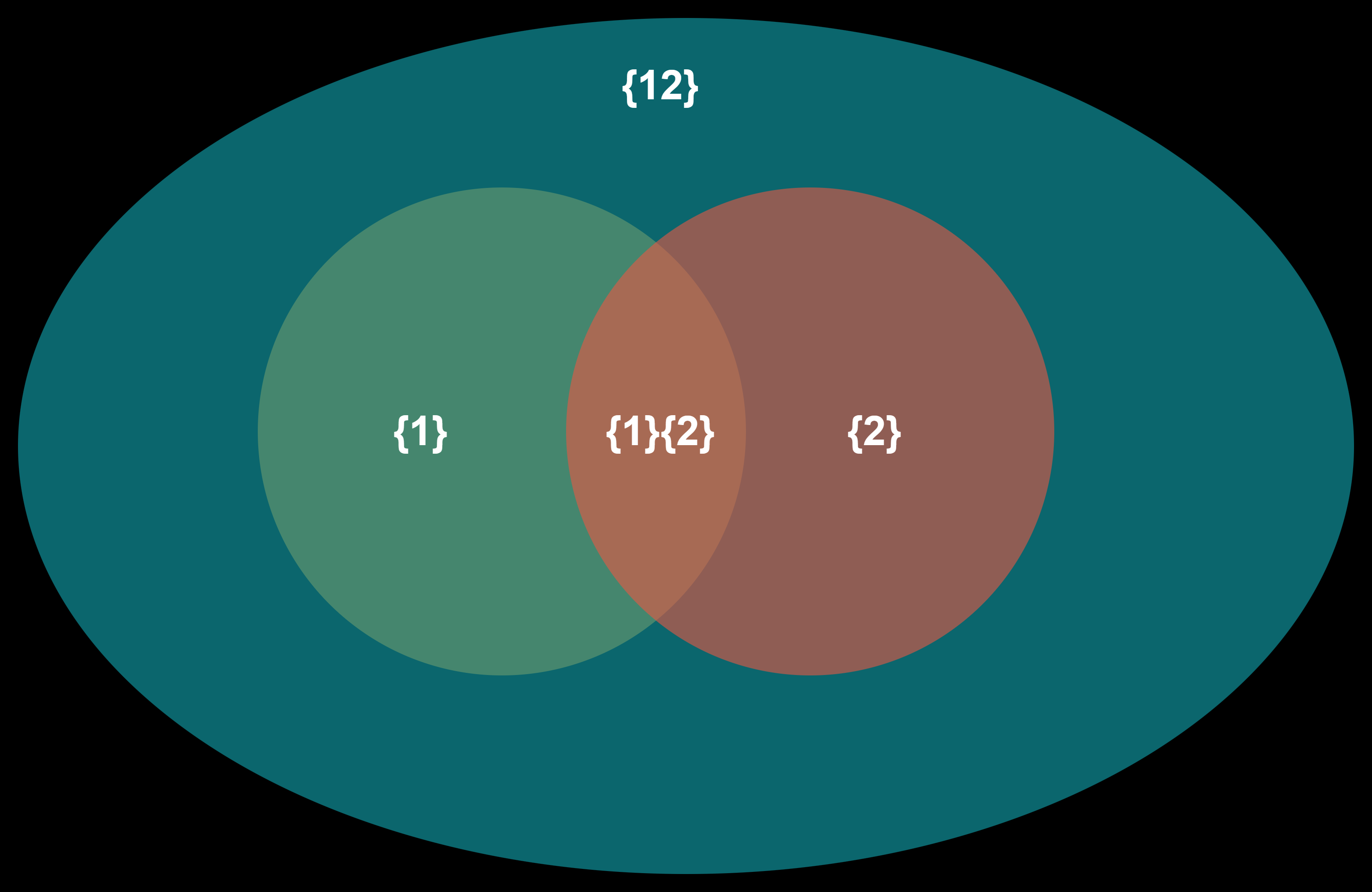
注:此处呈现包含关系,如{1}并非排除交集{1}{2}的部分,而是包含这一部分
晶格形式
左图A中的节点与文氏图中的部分一一对应,因而从下到上的节点积累的信息递增,类似$\sum$
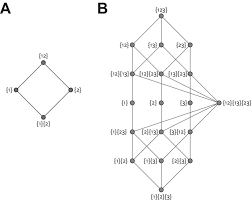
联系右图即可扩张到三维,分别给出了晶格形式和文氏图形式
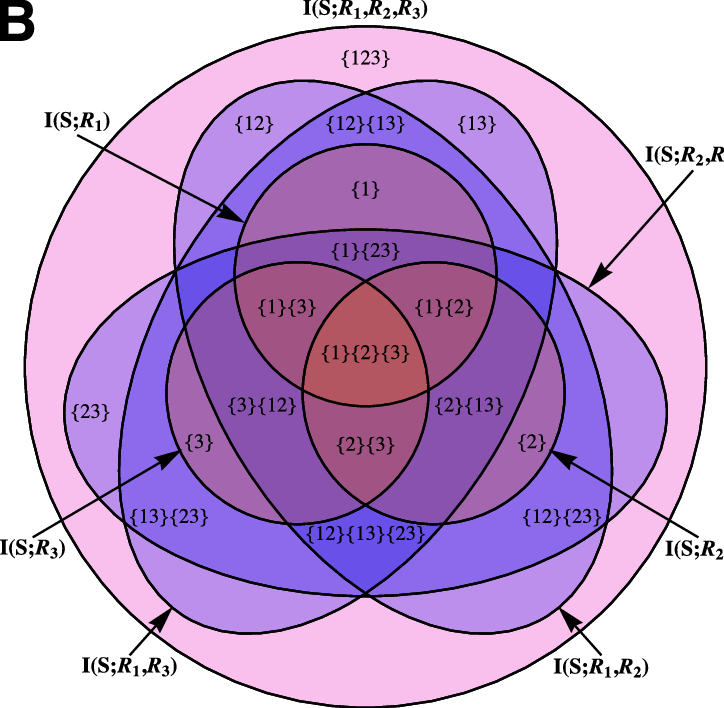
信息分解
$$\prod_R(S;A_i)=I_{\min}(S;A_i)-\sum_{A_j<A_i}\prod_R(S;A_j)$$
可以直观理解为这一节点增加的信息,类似$\delta$
计算得出
$$\prod_R(S;{1}{2})=0.311bit$$ $$\prod_R(S;{1})=0bit$$ 即为$R_1$ unique information $$\prod_R(S;{2})=0bit$$ $$\prod_R(S;{1,2})=0.5bit$$ 即为$R_1$ 和 $R_2$ synergistic information
因果涌现
Emergence as the conversion of information: A unifying theory这篇文章在此做了延伸,描述了信息分解之一框架下因果涌现的定义
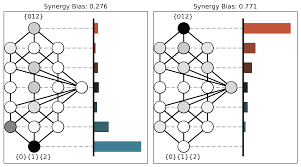
顶端的节点有着以下特点
- 最上面
- 最高维
- 最多的信息
- 最微观
- 最细粒化
注:两边的系统都是粗粒化过的,均揉成了3个节点
左侧下层的信息量很多,上层的信息量较少,因而下层共享了很多冗余信息量
右侧下层的信息量很少,上层的信息量较多,因而需要联合考虑、观察才能准确预测目标变量的状况
左侧是偏向冗余的系统,右侧是偏向协同的系统
节点之间相互作用比较冗余的更容易发生因果涌现
结论
- 目标是量化多变量作用于一个变量时,变量之间的信息结构
- 从定义冗余信息的视角开始量化过程
- 引入了信息晶格的定义
- 延伸出了信息分解的计算方法
- 最终可以量化每一个节点的信息贡献